Skip to article frontmatterSkip to article content

Example -2 Introduction to t-SNE for Clustering Visualization

This notebook demonstrates how to use t-Distributed Stochastic Neighbor Embedding (t-SNE) to perform dimensionality reduction and visualize clustering relationships among organisms based on their phenotypic growth predictions. The process involves reducing high-dimensional data into a 2D space to identify clusters and relationships visually.

Step 1: Load Necessary Libraries

We import essential Python libraries:

  • pandas: For data manipulation and loading tabular data.
  • matplotlib: For plotting the clustering results.
  • sklearn.manifold.TSNE: For dimensionality reduction using t-SNE.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.manifold import TSNE

Step 2: Load the Data

We load two phenotype prediction datasets:

  • ENIGMA dataset (couresty of ENIGMA group, and Hira Lesea)
  • PMI dataset (courtesy of PMI group, and Ranjan Priya)

The first column of each dataset is set as the index (organism names).

# Load the data
enigma_data = pd.read_csv('ENIGMA_phenoPredictions_CompleteM.tsv', sep='\t', index_col=0)
pmi_data = pd.read_csv('PMI_phenoPredictions_CompleteM.tsv', sep='\t', index_col=0)

Step 3: Label and Combine the Datasets

Each dataset is labeled to indicate its source (ENIGMA or PMI), and then the two datasets are combined into a single DataFrame to facilitate unified analysis.

# Label the datasets
enigma_data['Dataset'] = 'ENIGMA'
pmi_data['Dataset'] = 'PMI'
# Combine the datasets
combined_data = pd.concat([enigma_data, pmi_data])

Step 4: Prepare Data for t-SNE

We separate the dataset labels (used for coloring in the visualization) and the binary growth prediction data. The latter is used as the feature matrix for dimensionality reduction.

# Separate the 'Dataset' column for coloring and drop it from the feature matrix
labels = combined_data['Dataset']
feature_matrix = combined_data.drop(columns=['Dataset'])

Step 5: Perform t-SNE Dimensionality Reduction

We use t-SNE to reduce the high-dimensional feature matrix to 2D. This reduction:

  • Helps identify clusters of similar organisms.
  • Preserves local and global structure in the data.
  • Creates a visually interpretable 2D representation.
# Perform t-SNE to reduce dimensions to 2D
tsne = TSNE(n_components=2, random_state=42, perplexity=30, n_iter=300)
#tsne = TSNE(n_components=2, perplexity=30, n_iter=300)
tsne_results = tsne.fit_transform(feature_matrix)
/srv/conda/envs/notebook/lib/python3.11/site-packages/sklearn/manifold/_t_sne.py:1164: FutureWarning: 'n_iter' was renamed to 'max_iter' in version 1.5 and will be removed in 1.7.
  warnings.warn(

t-SNE Initialization: TSNE(n_components=2, random_state=42, perplexity=30, n_iter=300)

The TSNE object is initialized with the following parameters:

  • n_components=2:

    • Specifies the number of dimensions in the output space.
    • The high-dimensional input data will be reduced to 2 dimensions, typically for visualization purposes.

  • random_state=42:

    • Ensures reproducibility by setting a fixed seed for randomness.
    • Without this parameter, the results may vary slightly between runs due to the stochastic nature of t-SNE.
    • The value 42 is commonly used in data science as a default seed, but any fixed integer can be used.

  • perplexity=30:

    • Controls the balance between local and global data structure.
    • Determines the number of effective neighbors each data point considers.
    • Typical values range between 5 and 50, depending on the dataset size (smaller perplexity for smaller datasets).

  • n_iter=300:

    • Specifies the number of optimization iterations to refine the t-SNE representation.
    • Higher values may produce better results at the cost of longer computation time.

Fit and Transform: tsne.fit_transform(feature_matrix)

This step applies t-SNE to the input data (feature_matrix) and transforms it into the lower-dimensional space:

  • feature_matrix:

    • Represents the high-dimensional data to be reduced.
    • Each row corresponds to an individual data point (e.g., an organism).
    • Each column corresponds to a feature (e.g., growth prediction for a specific carbon source).

  • fit_transform():

    • Fits the t-SNE model to the feature_matrix.
    • Transforms the high-dimensional input data into a 2D space.

  • Output:

    • The result (tsne_results) is a NumPy array of shape (n_samples, 2), where:
      • n_samples: Number of rows in the input data.
      • 2: Number of reduced dimensions (as specified by n_components).
    • Each row in the result represents a data point in the 2D t-SNE space, preserving the structure and relationships of the original high-dimensional data.

Example Output

If the input feature_matrix contains growth predictions for 100 organisms across 50 features (carbon sources):

  • Input: A matrix of shape (100, 50) (100 rows, 50 columns).
  • Output: A 2D matrix of shape (100, 2), where each organism is represented by a point in the 2D space.

Step 6: Visualize the t-SNE Results

We plot the t-SNE results as a scatter plot. Points (organisms) are color-coded based on their dataset of origin (ENIGMA or PMI), making it easier to distinguish between groups and identify clusters.

# Convert results to a DataFrame for easy plotting
tsne_df = pd.DataFrame(tsne_results, columns=['t-SNE 1', 't-SNE 2'])
tsne_df['Dataset'] = labels.values

Visualize the t-SNE Clusters

  • Scatter Plot: Organisms are visualized as points in the 2D t-SNE space.
  • Color Coding: Points are colored by dataset type:
    • Blue for ENIGMA.
    • Green for PMI.
  • Labels:
    • t-SNE 1 and t-SNE 2 represent the reduced dimensions.
    • The legend distinguishes between the datasets.
# Plotting the t-SNE results with color coding for each dataset
plt.figure(figsize=(10, 8))
colors = {'ENIGMA': 'blue', 'PMI': 'green'}

for dataset in colors:
    subset = tsne_df[tsne_df['Dataset'] == dataset]
    plt.scatter(subset['t-SNE 1'], subset['t-SNE 2'], s=50, alpha=0.7, label=dataset, color=colors[dataset])

plt.title("t-SNE Plot of Organisms Based on Growth Predictions Across Carbon Sources")
plt.xlabel("t-SNE 1")
plt.ylabel("t-SNE 2")
plt.legend(title='Dataset')
plt.show()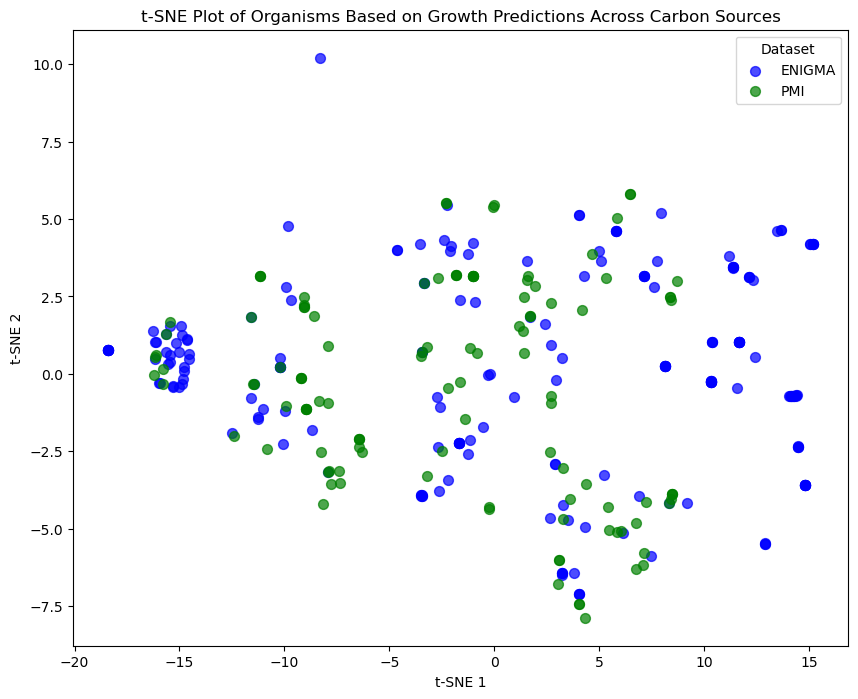
<Figure size 1000x800 with 1 Axes>

Explanation of the Code

1. What is Happening?

This code iterates over dataset types (e.g., ENIGMA and PMI) to plot points in a 2D t-SNE space. The steps include:

  • Filtering the data for each dataset type.
  • Plotting the points with specific colors and labels for differentiation.

2. Explanation of Each Line

for dataset in colors:

  • What It Does: Iterates over the colors dictionary where:
    • Keys represent dataset types (e.g., 'ENIGMA', 'PMI').
    • Values represent colors assigned to those datasets (e.g., 'blue', 'green').

subset = tsne_df[tsne_df['Dataset'] == dataset]

  • What It Does:
    • Filters the tsne_df DataFrame to select only rows belonging to the current dataset.
  • Why It’s Needed:
    • Ensures points from each dataset are plotted separately with their own color.

plt.scatter(subset['t-SNE 1'], subset['t-SNE 2'], s=50, alpha=0.7, label=dataset, color=colors[dataset])

  • What It Does:

    • Plots a scatter plot of points for the current dataset in the 2D t-SNE space.

  • Parameters:

    • subset['t-SNE 1'], subset['t-SNE 2']: The x and y coordinates in the reduced 2D space.
    • s=50: Sets the point size to 50.
    • alpha=0.7: Adds transparency to the points for better visualization of overlaps.
    • label=dataset: Adds a legend label for the dataset.
    • color=colors[dataset]: Assigns the predefined color to the dataset.

3. What Does It Accomplish?

This loop creates a scatter plot where:

  • Points for each dataset (e.g., ENIGMA and PMI) are plotted in 2D t-SNE space.
  • Each dataset is visually distinguished using:
    • Color (e.g., blue for ENIGMA, green for PMI).
    • Legend labels indicating the dataset type.
  • Transparency (alpha=0.7) makes overlapping points easier to interpret.

About t-SNE Plot

  • Purpose: The t-SNE plot provides an intuitive way to visualize high-dimensional relationships.

    • Organisms with similar growth patterns (e.g., similar ability to utilize carbon sources) cluster together in the 2D space.

  • Interpretation:

    • Clusters: Indicate groups of organisms with similar phenotypic profiles.
    • Outliers: Represent unique organisms with distinct growth patterns.

  • Applications: This technique is widely used in biology for:

    • Clustering phenotypic or genetic data.
    • Exploratory data analysis in other fields.
KBase (Biology)
Example 1 - Visualize phenotype prediction data
KBase (Biology)
Example 3: Clustering Analysis